什么?象棋和围棋都存在不败策略?
象棋和围棋都是中华文明的瑰宝 , 更是训练和测试思维能力的方式之一 , 那些在这两种棋类上取得成就的人们 , 其智商普遍得到公众认可 。但是 , 我们是否想过 , 在这两种棋类上是否存在必胜或者平局的策略?答案是存在的 , 这是策梅洛关于双人完全信息博弈的一个定理的结论 。本文将详细介绍这个定理的证明 , 并将其用于诸如五子棋的分析中 。如无特殊说明 , 后文所提及的游戏都是双人游戏 。
什么是最优策略
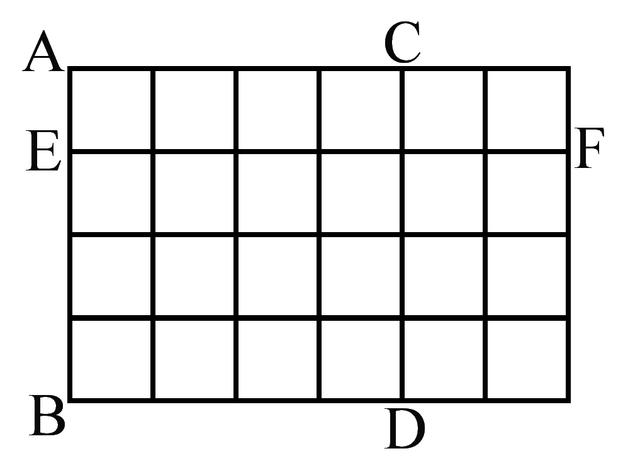
为了让大家对最优策略有一个直观的理解 , 这里举一个小游戏作为例子 。这个小游戏叫Chop , 在游戏的最开始有一个m×n的网格(下图是一个4×6网格示例) , 游戏由两位玩家轮流操作 , 每位玩家每轮可以沿着一整根竖网格线或者一整根横网格线将网格割掉一块 , 割到只剩下一个小方格的玩家为胜者 。注意 , 不能沿着剩余网格的边界线做切割 , 例如不能沿着下图的AB线切割 , 但是沿着CD线或者EF线切割都是可以的 。每次切割完之后网格会被分成两块 , 由操作切割的玩家决定留下哪一块 。
文章图片
文章图片
对于这类双人游戏 , 一般会有最先进行操作的玩家 , 我们将其称为先手 , 另一位被称为后手 。如果一开始的时候m和n其中一个数为1 , 比如n=1 , 先手玩家可以直接切割掉(m-1)个格子即可获得胜利 , 这个策略就是先手玩家的最优策略 。如果对于一般的m和n , 先手或者后手怎样才能保证获胜呢?读者可以稍作思考 , 再接着往下看 。
其实很简单 , 如果m和n不相等 , 那么先手的最优策略会导致必胜的结果:这时候先手玩家只要割掉其中一块使得剩下的网格是个长和宽相等的网格即可 。这样 , 无论后手切割哪条线 , 都是在长和宽相等的基础上进行切割 , 最后必然得到一个长宽不相等的网格 , 也就不可能是单独一个网格 。先手玩家只要每一步实行这个策略 , 无论后手玩家怎么操作 , 先手玩家都会获胜 。这时候读者肯定明白了 , 当m=n的时候 , 无论先手玩家怎么操作 , 后手玩家都可以借助前述一样的策略获胜 。
完全信息博弈和策梅洛定理
现在回到一般游戏的讨论上 。策梅洛定理适用于被称为完全信息博弈的一类游戏 。所谓完全信息博弈 , 指的是游戏的所有信息都是公开的 , 游戏双方都能清楚了解到目前游戏所处的状态信息 , 并且游戏的每一步都不涉及概率因素 。这个条件把扑克、飞行棋、暗棋和翻棋玩法下的军棋都排除掉了 。然后 , 我们还需要这个游戏能在有限步内结束 , 并且 , 游戏的结局要么是平局要么有一方是胜者 。很明显 , 围棋是属于完全信息博弈的 。至于象棋 , 有可能会进入循环状态从而整个游戏没完没了 。为了避免这一点 , 我们可以加入一些新规则使得象棋不会出现循环 , 比如 , 设定一个很大的数N , 只要连续N步双方都没有被吃掉棋子就判为和棋 , 或者不允许超过N次进入同一种棋子状态 , 否则判为和棋 。加入这些规则或者类似的规则之后 , 象棋就满足要求了 。
下面给出策梅洛定理的严格表述:在双人完全信息博弈下 , 只有三种情况:要么先手具有必胜策略 , 要么后手具有必胜策略 , 要么双方的最优策略会导致平局 。比如前面所说的Chop游戏 , 当m≠n时 , 先手玩家具有必胜策略;如果m=n , 后手玩家具有必胜策略 。Chop游戏没有平局 。策梅洛定理是一个结论很强的定理 , 下面我们会发现 , 它的证明非常简单 , 不需要用到很高深的知识 。
推荐阅读
- 老公为什么会找丑的女人做女朋友?
- 一个女人,如果她什么都懂,那她一定恋爱过
- 吴婷和武庚的婚姻是否能够帮助他人的婚姻?
- 嫁给一个不爱自己的男人是什么感受?
- 女人主动加男生微信,这没什么不合适
- 为什么有些女人不肯承认老公还爱自己?
- 喜欢上一个人的时候,男方和女方各是如何说的
- 婚姻里,男人最害怕的事情是什么?
- 嫁对人和嫁错人,是完全不同的两种人生
- 为什么说三个月是分手魔咒?












