“社交牛X症”发病原因的数学分析( 二 )
文章图片
文章图片
考林西(左)与米尔格拉姆(右)(图片来源:wikipedia)
米尔格拉姆最初以美国堪萨斯州威奇托市为起点 , 随机选择了60名志愿者 , 他给了每位志愿者一封信 , 并要求志愿者将信传递给一位居住在马萨诸塞州某指定地点的股票经纪人 。早期的实验虽然设计比较粗糙 , 但仍然有3封信送到了目的地 。后经过多次改良实验 , 米尔格拉姆成功将送达率提升至35% , 后来更上升为97% 。

文章图片
文章图片
米尔格拉姆实验中一条可能的传递路径(图片来源:wikipedia)
不仅如此 , 米尔格拉姆还发现了所谓的漏斗效应 , 即大部分的传递都是由那些极少数的明星人物完成的 。在一次样本数为160的实验中 , 24封信最终送到收信人的家中 , 其中16封会经同一人送到;剩下的送到收信人办公室的信件中 , 也有一半是由两个人送来的 。
这些实验 , 为后来小世界网络的严格建模提供了支持 。
小世界网络的数学基础
小世界网络在社会学研究中被提出后 , 在相当长的时间里都没有与之相对应的数学模型 。直到1998年 , 当时还在康奈尔大学攻读博士学位的邓肯·瓦茨(Duncan Watts)与导师斯蒂文·斯特罗加茨(Steven Strogatz)提出了一种新的复杂网络模型 , 即著名的瓦茨-斯特罗加茨(WS)模型 , 这也是最经典的小世界网络模型 。

文章图片
文章图片

文章图片
文章图片
瓦茨(左)与斯特罗加茨(右) 邓肯·瓦茨 , 宾夕法尼亚大学教授 , 曾任微软纽约研究院首席研究员 。斯蒂文·斯特罗加茨 , 康奈尔大学教授 , 同时也是一位科普作家 。(图片来源:wikipedia、stevenstrogatz.com)
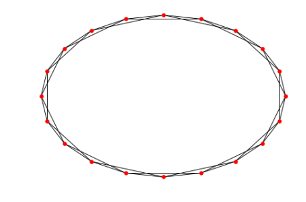
WS模型首先定义了一个初始状态(规则网络) , 即每个节点都与一定距离的节点相连 , 也就是社交的初始状态——首先与邻居交朋友 。假设节点数为N(即研究对象总共有N个人) , “邻居”定义为与此节点最近的2k个节点 。此外 , 我们还要求k远小于N 。多言无益 , 直接上图——
文章图片
文章图片
文章图片
文章图片
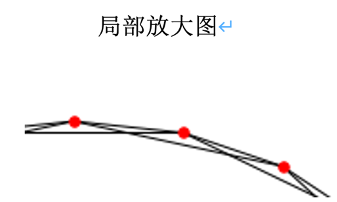
N=20(共有20个红点) , k=2(左右两侧各2个 , 共计4个"邻居") , p=0(所有连接都不会被重连)
接下来 , 选择规则网络中的一个节点(标记为1号) , 从它开始将所有节点顺时针编号 。然后1号节点的第1条连接会有0
文章图片
文章图片
N=20 , k=2 , p=0.5(即每条连接有50%概率被重连)
当然我们也可以让这个过程极端一些 , 譬如令p=1 , 我们将得到一张更为混乱的图 , 即随机网络 。

文章图片
文章图片
N=20 , k=2 , p=1(即每条连接都被重连)
“病因”大揭秘
推荐阅读
- 爱心义诊“进家门”!苏州市相城区黄桥街道方浜村贴心服务暖民心
- 连烧数月难寻因 河南小伙肺毁损 医生耗时一个月摸到发烧“开关”小伙写千字长文妙语连珠谢医护
- 常敲“一氧化碳中毒”警钟 科学防范 温暖过冬
- 博爱县月山镇:凝心聚力改善人居环境 村庄“旧貌换新颜”
- 广西中医药大学第一附属医院:“内”“外”兼并 大力弘扬中医药文化
- 夫妻“小别重逢”过后,男人会有这两个表现
- 新冠肺炎患者集中康复出院 “白衣战士”画新作:“相信阳光离我们不远了”
- 新春走基层丨杨国贵:“养牛倌”走上致富路
- 信阳浉河区:宜居环境助力幸福生活“节节高”
- 只想躺平?您可能是病了!“工作倦怠”正式成为疾病
















