“社交牛X症”发病原因的数学分析( 三 )
有了上面的一系列铺垫 , 让我们最终步入正题 , 看看所谓的社交牛X症的发病原因 , 及其背后的数学原理 。
首先让我们考虑社交达人所具有的属性 。有人可能会觉得 , 社交牛X症患者必定朋友多多 。但根据英国人类学家罗宾·邓巴的研究 , 一个人维持紧密人际关系的人数是有上限的 , 一般而言为150左右 。换言之 , 有些人虽然“认识”很多人 , 但不能建立更进一步的关系 。所以相较于朋友的数量 , 朋友圈整体质量更能反映一个人社交牛X的程度 。

文章图片
文章图片
敢于乱搭讪并不能证明你就是社交牛X症 , 因为——

文章图片
文章图片
所以在本研究中 , 我们沿用WS模型的设定 , 假设每个节点的邻居都为2k 。同时定义“所有与某节点相连的点之间的实际边数 , 除以这些点之间可能存在的边数的最大值”为集聚系数(编者注:可反映节点之间结集成团的程度) 。为了方便大家理解 , 把上面的定义写成简单的数学表达式:

文章图片
文章图片
没看明白?点击捋思路
点此展开
更具体的解答

文章图片
文章图片
为了方便理解 , 这里再举一个例子 。取最简单的情况 , p=0 , k=3 , 上图中红点定义为点i , Cimax=蓝色边+黑色边 , Ni=黑色边 。对于最简单的情况 , p=0(规则网络) , 我们可以利用小学数学知识(这里真的是小学数学——植树问题的变种有木有) , 计算Ci 。

文章图片
文章图片
由于规则网络中每个点的情况都是相同的 , 所以整个网络中所有节点的集聚系数的平均值也等于上面得到的Ci 。而对于一般情况 , 当p>0时 , 我们也可以求得每个点的集聚系数和整张网络的平均集聚系数 。根据Barrat和Weigt的数值模拟 , 网络的平均集聚系数可以近似地记作:
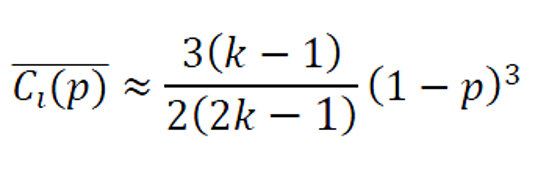
文章图片
文章图片
类似地 , 我们可以定义节点间的路径长度dij , 进而求得整个网络所有节点间的平均路径长度L 。平均路径长度指示了网络中两点间最短距离的平均值 。

文章图片
文章图片
值得一提的是 , 对于社交网络(也就是图论研究的图)而言 , 存在有向图(与节点相联的边有出入之分)和无向图两种情况 。上面介绍的结论皆是以无向图作为研究对象 , 但有向图的分析方法类似 , 只是需要区分dij与dji 。

文章图片
文章图片

文章图片
文章图片
无向图(“你爱我呀我爱你”)vs有向图(“你不要过来啊”)(图片来源:giphy.com)
推荐阅读
- 爱心义诊“进家门”!苏州市相城区黄桥街道方浜村贴心服务暖民心
- 连烧数月难寻因 河南小伙肺毁损 医生耗时一个月摸到发烧“开关”小伙写千字长文妙语连珠谢医护
- 常敲“一氧化碳中毒”警钟 科学防范 温暖过冬
- 博爱县月山镇:凝心聚力改善人居环境 村庄“旧貌换新颜”
- 广西中医药大学第一附属医院:“内”“外”兼并 大力弘扬中医药文化
- 夫妻“小别重逢”过后,男人会有这两个表现
- 新冠肺炎患者集中康复出院 “白衣战士”画新作:“相信阳光离我们不远了”
- 新春走基层丨杨国贵:“养牛倌”走上致富路
- 信阳浉河区:宜居环境助力幸福生活“节节高”
- 只想躺平?您可能是病了!“工作倦怠”正式成为疾病












