树的定义和逻辑结构(1)树的定义
树是n(n≥0)个结点的有限集T , n=0称为空树 , n>0 为非空树 。 非空树中:
1.有且仅有一个称为根的结点;
2.当n>1时 , 其余结点可分为m个互不相交的有限集T1、T2、… 、Tm , 而每一个Ti(i=1,2,…,m) 也是一棵树 。 Ti称为根的子树 。
(2)树的逻辑结构
1.树中根结点的任意一个直接后继结点及该结点的所有后继结点也是以该结点为根的一棵树;
【计算机中树的度和算法 树的度是啥意思怎么算】2.根结点没有前驱结点 , 其他结点有且仅有一个直接前驱结点;
3.每一个结点可以有零个或多个后继结点;
4.树型结构的元素间存在一对多的关系 。
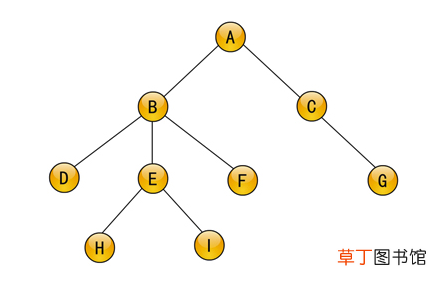
如图6-1所示的一棵树T 。
它由根结点A和两棵子树T1和T2所组成 , T1和T2分别位于A结点的左下部和右下部 , 其中树根结点A是两棵子树的根结点B和C的前驱 , 相反B和C是A的后继;
T1又由它的根结点B和三棵子树T11、T12和T13所组成 , 这三棵子树分别位于B结点的左下部、中下部和右下部 , 其中B结点是这三棵子树的根结点D、E和F的前驱 , 相反它们都是B的后继;T11和T13只含有根结点 , 不含有子树(或者说子树为空树) , 不可再分;T12又由它的根结点E和两棵只含有根结点的子树所组成 , 每棵子树的根结点分别为H和I , E是H和I的前驱 , 而H和I均是E的后继;T2由它的根结点C和一棵子树所组成 , 该子树也只含有一个根结点G , 不可再分 。
文章插图
树的逻辑结构
树的基本术语(1)结点的度和树的度
一个结点的子树的数目或者说该结点引出的边数被定义为该结点的度(Degree) 。 树中所有结点的度的最大值被定义为该树的度 。 如在图6-1的树中 , B结点的度为3 , A、E结点的度均为2 , C结点的度为1 , 其余结点的度均为0 。 因所有结点的最大的度为3 , 所以树的度为3 。
(2)分支结点和叶子结点
在一棵树中 , 度等于0的结点称作叶子结点或终端结点 , 度大于0的结点称作分支结点或非终端结点 。 在分支结点中 , 每个结点的分支数就是该结点的度数 , 如对于度为1的结点 , 其分支数为1 , 又称为单分支结点;对于度为2的结点 , 其分支数为2 , 又称为双分支结点 , 其余类推 。 如在图6-1的树中 , D、H、I、F、G为叶子结点;A、B、C、E为分支结点 , 其中C为单分支结点 , A和E为双分支结点 , B为三分支结点 。
(3)孩子结点、双亲结点和兄弟结点
在一棵树中 , 每个结点的子树的根 , 或者说每个结点的后继 , 被习惯地称为孩子、儿子或子女(Child) , 相应地 , 把该结点称为孩子结点的双亲、父亲或父母(Parent) 。 具有同一双亲的孩子互称为兄弟(Brothers) 。 每个结点的所有子树中的结点被称为该结点的子孙 。 每个结点的祖先则被定义为从整个树的根结点到达该结点的路径上所经过的全部分支结点 。 如在图6-1的树中 , B结点的孩子为D、E、F结点 , 双亲为A结点 , D、E、F结点互为兄弟 , B结点的子孙为D、E、H、I、F结点 , I结点的祖先为A、B、E结点 。 对于图6-1树中的其他结点亦可进行类似的分析 。
推荐阅读
- 沙棘树的生长环境和植物种类 沙棘是一种什么植物
- 阴历生日的算法 怎么计算自己农历生日
- 中旬的意思和时候计算方式 中旬是什么时候开始算
- 带货坑位费的意思和计算方式 坑位费是什么意思
- 考拉吃桉树叶的原因 桉树叶有毒为什么考拉吃
- 我国各地秋天的计算月份 几月是秋天
- 新高考等级赋分制的计算划分方式 等级赋分是什么意思
- 衣服上松树油洗掉的处理方法 松树油怎么能洗掉
- 十年树木的下一句 十年树木整首诗
- 千树万树梨花开的上下句及全诗含义 千树万树梨花开的上一句













